Создание парабол
|
<< Оглавление >> Создание парабол |
  
|
Возможности:
1) Симметричная (обычная) парабола
2) Сопрячь элементы параболой.
Запрашиваются по одному 2 элемента,
далее есть 3 варианта: Укажите радиус или [Длина проекции/Точка].
Если не построилось сопряжение по радиусу – радиус задан слишком маленький.
При указании способа Точка поддерживается динамическая отрисовка.
Операция зациклена.
3) Построение асимметричной параболы

Примечание: сопряжений для нее не хватает, и редактирование, следовательно, не полное.
4) Сопрячь прямые асимметричной параболой.
Парабола
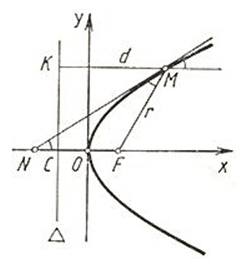
Пусть на плоскости заданы точка F и прямая ![]() , не проходящая через F. Парабола – множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой
, не проходящая через F. Парабола – множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой ![]() . Точка F называется фокусом, прямая
. Точка F называется фокусом, прямая ![]() – директрисой параболы; (OF) – ось, O – вершина,
– директрисой параболы; (OF) – ось, O – вершина, ![]() – параметр,
– параметр, ![]() – фокус,
– фокус, ![]() – фокальный радиус.
– фокальный радиус.
Каноническое уравнение: ![]()
Эксцентриситет: 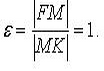
Фокальный радиус: ![]()
Уравнение директрисы: ![]()
Уравнение касательной в точке ![]()
![]()
Свойство касательной к параболе: 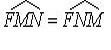 (М – точка касания; N – точка пересечения касательной с осью Ox).
(М – точка касания; N – точка пересечения касательной с осью Ox).
Уравнение нормали в точке ![]()
![]()
Уравнение диаметра, сопряженного хордам с угловым коэффициентом k: y = p/k.
Параметрические уравнения параболы: ![]()
Полярное уравнение: ![]()